Spinning Universe - Introduction

Main Menu

Articles

Introduction to SpinningUniverse.com

INTRODUCTION TO SPINNINGUNIVERSE.COM
By Puthalath Koroth Raghuprasad
Odessa, Texas
Contact Us or Leave Comment

THE ORIGIN AND PERSISTENCE OF CELESTIAL BODY MOTIONS IN THE UNIVERSE

ABSTRACT

In this paper we present the factors that lead to the generation of motions of celestial bodies, and how and why they become permanent. Foremost among our findings is a linear relationship between the mass of the solar system planets and their axial rotation rates. This relationship between the size of a body and its ability to rotate on its axis is displayed by the smallest (satellites), all the way to the largest bodies and conglomerations of matter (the galaxies). This is dramatically demonstrated by the fact that the satellites and planets rotate on their axes at so many kilometers per hour, whereas the stars and galaxies clock at kilometers per second! And larger galaxies (“Super Spirals”) rotate on their axes much faster than the smaller ones. The takeaway from the above is that the axial rotation of celestial bodies is an inherent, autonomous property, akin to their equally ubiquitous mutual gravitation. Clearly, all motions begin with this innate ability of matter to spin. When one considers the fact that all fundamental particles spin on their axes and the protoplanetary disk is already spinning on its axis, it is clearly a property that spans the whole spectrum of matter, in the nano world as well as the macro world. Next, all bodies rotate in the counterclockwise direction and all satellites orbit mother bodies also in the counterclockwise direction, which hints at mother bodies’ role in guiding the satellites’ motions. Also, the proximal, synchronously rotating satellites of larger mother bodies orbit faster than the satellites of smaller, slower rotating mother bodies. Similarly, the axial rotation speed of the satellites of larger mother bodies is greater than that of the satellites of smaller mother bodies. These critical observations hint at a direct effect emanating from mother bodies, through combining the gravity and axial rotation, with the intent of both guiding the direction of and the speed of orbit and even the axial rotation speeds of respective most proximal satellites. This control is evident in the closest satellites displaying minimal axial tilts, and rotating synchronously, while those satellites that are situated at intermediate distances displaying increasing axial tilts and rotating non-synchronously (normal); the axes of the satellites that are farthest from the mother bodies are inverted and they rotate negatively. From the data presented above we can now distil the intricate mechanisms involved in the motion mechanics of celestial bodies: All bodies have mutual gravitation to attract other bodies, the larger bodies attract more strongly smaller bodies in their vicinity, but only when this force is combined with axial rotation would meaningful motion mechanics begin. In this, gravity helps grab the satellites, the axial rotation of the mother body then enables the satellites' orbits. This circular motion uses the resulting centrifugal force to prevent the bodies from crashing into the mother bodies. Finally, for all these motions to proceed fluidly, the near perfect vacuum and the weightlessness of bodies in deep space are complimentary. It is not known if the extreme cold in those locations has any role to play. Finer details of how such purposeful collaborative actions take place and help initiate and continue in perpetuity all motion mechanics in celestial bodies will be explained later in the paper, without resorting to complex mathematical computations or invoking esoteric, imaginary forces and properties of bodies, or the presence of unseen matter outside of the bodies or conglomerates of bodies. Our prior papers have dealt with aspects of the ideas presented in this paper; thus, this can be considered a summation of the components of the natural processes that result in the orderly motions of celestial bodies.

KEY WORDS

Celestial bodies, gravity, axial rotation, galaxies, satellites, synchronous and non-synchronous rotations

INTRODUCTION

All fundamental particles (1,2,3) spin on their axes and all celestial bodies of substantial mass rotate on their axes and orbit the nearby large body, and their orbits are along the ecliptic of mother bodies. In the macro world this is the one most readily observable property of matter, so much so the great mathematician/ astronomer of ancient India Aryabhata (476-550 CE) (4-8), suggested that the appearance of the “heavens rotating” around the earth was actually an illusion created by the earth rotating on its axis. In the Millennium and half since that observation, what makes the celestial bodies rotate on their axes has not been conclusively elucidated. Over the past three centuries the concept of a “conservation of the angular momentum” (2,3) had been accepted by most scientists. It is not clear to us from where this angular momentum originated and why it continues apparently for infinity. If it starts from the time of formation of the star, an appropriate question might be, what about the galaxies, which are also rotating on their axes, and even how would the Sun’s rotation impart that property to all fundamental particles, many of which are of extra-solar origin. We also had a hunch that mere mutual attraction of bodies due to gravity couldn’t explain the orderly movements of satellite bodies, only in the counterclockwise direction and only along the ecliptic of the mother. Since all bodies are rotating on their axes, we suspected that somehow gravity and axial rotation were cooperating in at least promoting the orderly movements of celestial bodies. To our surprise and satisfaction, our research of the literature and other sources of information provided many nuggets that helped us formulate our theory in which the basic participants in the motion mechanics are as we suspected but we had to add two factors that facilitate ease of movement; these are the almost perfect vacuum and the weightlessness of bodies that prevail at the locations where all celestial bodies are situated. Many of our discoveries were totally unexpected but much to our gratification, always they added to the body of evidence. Since all motions were almost circular, another common phenomenon, the centrifugal force, turns out is the force that acts against mutual gravitation, which concept was the most evasive part of the motion mechanics in modern astronomy teaching. Einstein's "Cosmological Constant" and many of the contemporary concepts such as negative energy were put forward to solve the riddle but clearly, centrifugal force, is the clever solution of nature.

METHODS AND OBSERVATIONS

The data presented in this paper were derived from exhaustive study of astronomical and astrophysical literature, both in print and online, as well as data available on the websites of NASA and other similar agencies. Since all bodies rotate on their axes and orbit larger bodies, naturally, our focus turned to data and articles dealing with these properties. Unfortunately, data dealing with axial rotation and its relationship with celestial body motion mechanics were indeed sparse; this was evidently due to the deep-rooted bias that those movements were due to “conservation of the angular momentum” and as such they played no purpose in astronomy, thus many of the crucial data we used were calculated from the available published material. However, we were able to obtain and present a cohesive narrative of how motion mechanics originate in the astronomical bodies in the universe, and why such motions do not decline and stop over time. As one would expect, much of the data are from solar system bodies and for obvious reasons, they are the most accurate. In contrast, accurate and reliable data on stars and galaxies were hard to obtain, especially those dealing with their motion characteristics. In the appropriate sections in this paper, we will point out such difficulties as we present them. Our observations will be presented in the following sections: the axial rotation characteristics of the solar system planets, the effects of the collaboration between gravity and axial rotation of bodies, followed by the interactions of mother bodies with their satellites, the unusual motion mechanics of some of the bodies and finally, available data on stars and galaxies’ motions.

Figure 1a below shows comparison of mass of the major solar system planets and their respective axial rotation rates. Notice we did not include Mercury and Venus as they had some unusual features that affect their rotation characteristics. Thus, both of them rotate extremely slowly, (Mercury rotates once in 1407.6 hours and Venus rotates once in 5832.6 hours). We believe the reasons for the inordinate delays are: in the case of Mercury it is due to the large amount of iron in its interior and thus, its movements are impacted by being next to an extremely magnetic Sun, whereas the movements of Venus are affected by its inverted axis (this is elaborated later on in this paper). Thus, listed in order of size are Mars, earth, Uranus, Neptune, Saturn and Jupiter. As can be seen, the larger the body, the faster it rotates on its axis. There is, in fact, a linear relationship between mass and rotation. This result is quite unexpected, as we expect larger bodies to be more sluggish. It also probably argues against the concept of “conservation of the angular momentum”, in which, with time, one would expect gradual slowing and even complete cessation of all rotation and other motions. The findings in this figure argue for an intrinsic and fundamental property of matter in the ability of the celestial bodies to rotate on their axes. The fact that all axial rotations are in the counterclockwise direction in all bodies speaks to the purposeful nature of this feature. Thus, we believe that this is, along with mutual gravitation, the most important and basic property of matter, when it comes to the motion mechanics.

Figure 1a
COMPARISON OF SPEED OF AXIAL ROTATION AND MASS OF
SELECTED SOLAR SYSTEM PLANETS

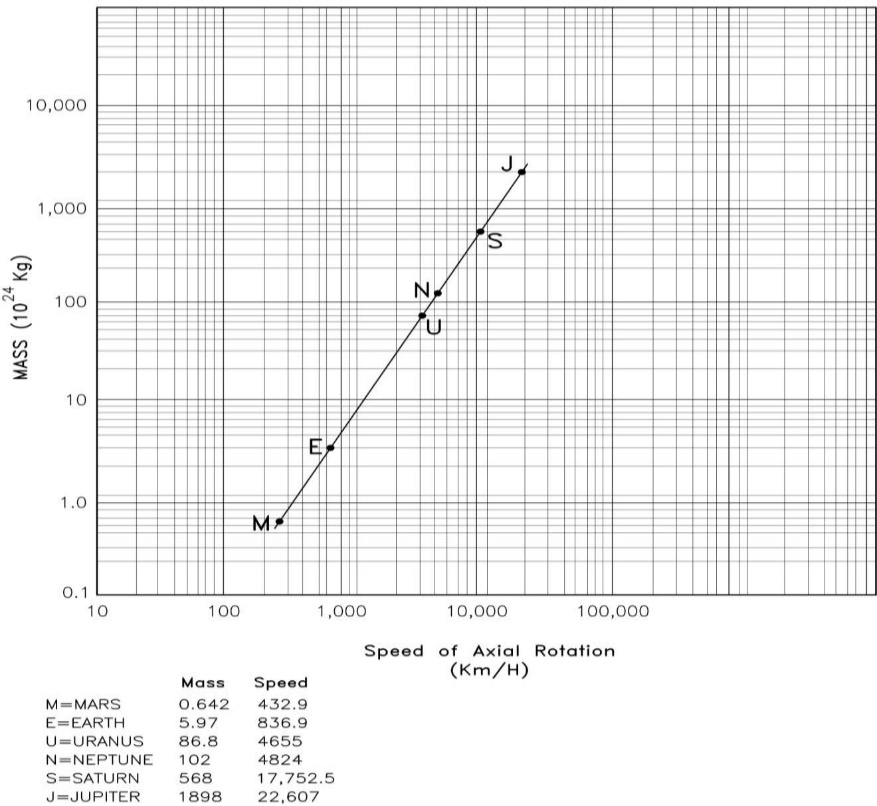
Chart, line chartDescription automatically generated

Adapted from http://www.nssdc.gsfc.nasa.gov/planetary/factsheet.htm
Reproduced from Applied Science and Innovative Research, www.scholink.org/ojs/index.php/asir Vol. 4,
No.3, 2020 (9)

Table 1 below explains how the axial rotation affects the equatorial radius and the presence or absence of magnetism. Thus, the planets that rotate slowly (Venus and the dwarf planet Pluto) do not have magnetism, and there is a rough correlation between the speed of axial rotation and the equatorial radius. The latter clearly teaches us that the axial rotation of bodies counteracts the inward push of gravity and help maintain the roughly spherical shape. We have explained in depth in our prior paper (9) how the magnetism is made in rotating celestial bodies, by the liquid metals and molten rock in the core of the planet remaining stationary but the hard matter in the outer layers is rotating around the axis and thus create electromagnetism.

Table 1. Equatorial Radii Compared to Polar Radii of Planets, and Axial Rotation Rates, as well
As Gravitation and the Presence of Magnetism in the Solar System Bodies

Measurement	Mercury	Venus	Earth	Mars	Jupiter	Saturn	Uranus	Neptune	Pluto
Eq. Rad (Km)	2439.7	6051.8	6378.1	3396.2	71,492	60,268	25,559	24,764	1188
Polar Rad (Km)	2439.7	6051.8	6356.8	3376.2	66,854	54,364	24,973	24,341	1188
Sider. Rot (Hrs)	1407.6	-5832.6*	23.9	24.6	9.93	10.7	-17.2*	16.1	-153.3*
Ax.Rot.Speed (Km/H)	10.88	6.52	1,677	867	45,255	35,550	9,319	10,231	49
Gravity (m/s²)	3.7	8.9	9.8	3.7	24.8	10.44	8.7	11	0.7
Magnetism	Yes	No	Yes	No	Yes	Yes	Yes	Yes	Unknown

* Negative values indicate retrograde rotation (spinning in the opposite direction compared to most planets)

Adapted from http://www.nssdc.gsfc.nasa.gov/planetary/factsheet.htm (18th March 2025)
Reproduced from Applied Science and Innovative Research, Vol. 4, No 3, http://dx.doi.org/10.22158/asir.v413p1 (9)

We show in Figure 1b below the degree of gravitation of all solar system planets (we have included the dwarf planet Pluto as well) and plotted against their sizes. There is a definite positive relationship between mass and gravity but unlike the axial rotation, the relationship is not linear. It is not clear why that is, but we suspect the reason is, unlike the axial rotation, the measurement of gravity is not as accurate and with more accurate measurements, we might show the exact same linear relationship with gravity as well.

Figure 1b

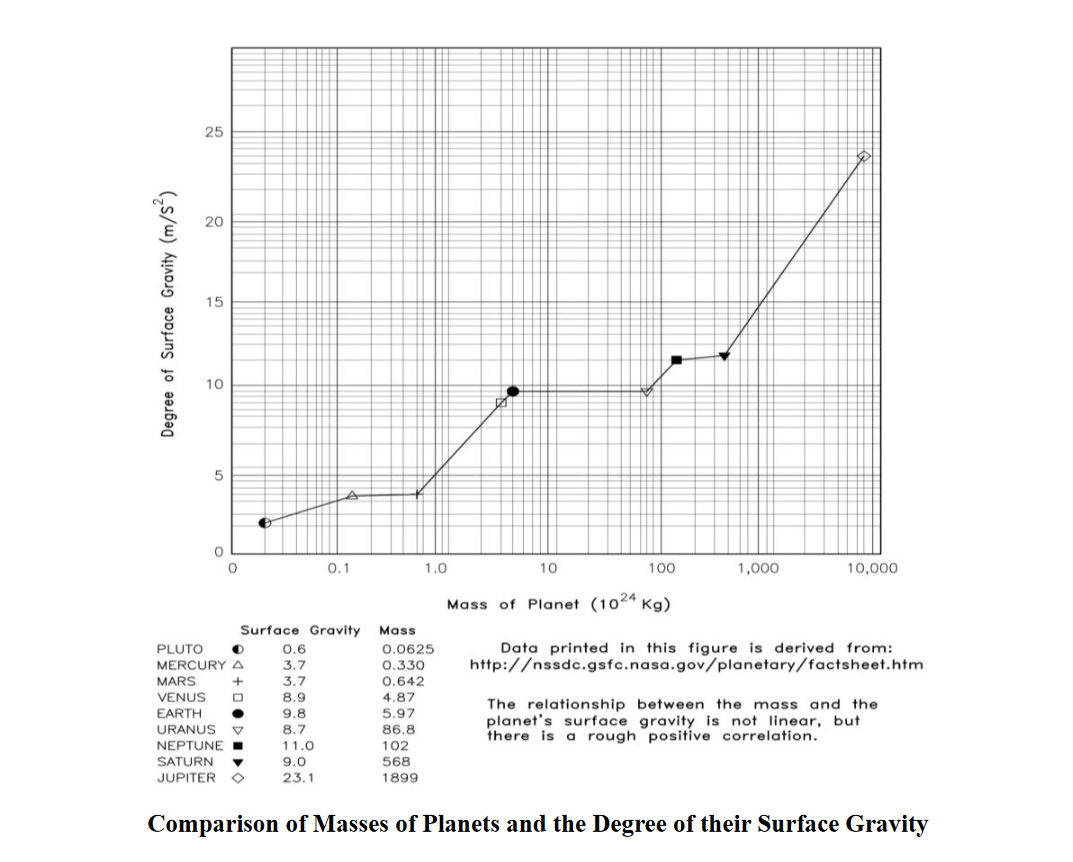
Reproduced from Applied Science and Innovative Research.Vol.4, No.3.2020 www.scholink.org/ojs/index.php/asir (9)

Next, we examine the effect the mother body has on its proximal, synchronously rotating satellites’ speed of orbit, as shown in Table 2. When there are multiple satellites, their individual orbital speeds are reported first and the average for each group is then given at the bottom of each group. The average for Mars’ satellites is 6,281 km/h, that for Uranus’ is 17,004 km/h, that for Neptune’s is 39,920, for Saturn’s is 40,920, and that for Jupiter’s it is 45,157 km/h. Thus, there is a rough correlation of the orbital speeds of these satellites to the mother bodies’ mass. Next, in each group, the closest satellite orbits the fastest and the farthest ones orbit the slowest. There is a tendency for the nearest satellites to be smaller than the farthest ones. It is not clear the implications of the last observation. To sum, the ability of mother bodies to make the satellites to orbit is clearly an influence quite apart from the pull of gravity; this is what we call a “rotational effect” from the mother to the satellites. The reason for earth’s solitary moon, while still synchronously rotating, to orbit slower than the satellites of Mars, despite the larger size of earth is most likely due to the greater distance from earth (Phobos 9.38 and Deimos 23.46 x103 km and moon 384.4 x 103 Km)

We infer from the above findings that mother bodies have a commanding role in determining both the direction of and the speed at which the satellites orbit. They also teach us that for such orderly motions to take place, both the gravity and the axial rotation of mother bodies work in tandem. Since both gravity and axial rotation are intrinsic properties of matter (as noted above), it is not surprising that their job is to initiate and continue celestial body motion mechanics. The orbits being in only counterclockwise direction assures orderly movements and decidedly less chaos. Why mother bodies influence the axial rotation of satellite bodies is unknown, as satellites do rotate on their own.

Table 2

PLANETARY AXIAL ROTATION RATES vs. SATELLITES’ ORBITAL SPEEDS (Synchronously Rotating Satellites)
PLANETS			SATELLITES
	MASS (10 24 Kg)	AXIAL ROT. SPEED (Km/hr)		DIST. FROM MOTHER (10 3km)	MASS*	ORBITAL SPEED (Km/hr)
1) Mars	0.642	867	Phobos Deimos	9.38 23.46	10.6 2.4	7,695 4,868 =6,281
2) Earth	5.97	1677	Moon	384.4	0.073	3,679
3)Uranus	86.8	9,310	Miranda Ariel Umbriel Titania Oberon	129.9 190.9 557 436 584	0.66 13.5 11.7 35.2 30.1	23,923 19,844 16,821 13,110 11,320 =17,004
4)Neptune	102	10,231	Naiad Thalassa Despina Galatea Larissa	23.2 25.2 27.7 37.2 48.8	0.002 0.004 0.02 0.04 0.05	43,350 42,129 41,045 37,836 35,238 =39,920
5) Saturn	568	17,775	Mimas Enceladus Tethys Dione Rhea	185.5 238 294.7 377.4 527	0.379 1.08 6.18 11.0 23.1	51,684 45,471 40,879 36,036 30,531 =40,920
6) Jupiter	1899	45,255	Io Europa Ganymede Calisto	421.6 670.9 1070 1883	893.2 480 1481.9 1075.9	62,382 49,613 39,103 29,531 =45,157

Adapted from: http://nssdc.gsfc.nasa.gov/planetary/factsheet and related pages.
Only for the moon was actual value derived from the NASA’s website; all other values were calculated from the values for the orbital parameters posted at the website. For calculating the orbits of the small satellites, where only semi-major axes were provided, they were used; since all satellites’ values were thus affected, we accepted that limitation.
  = followed by a number is the average of each planet’s satellites’ orbital speed. These values clearly demonstrate that the larger the planet, faster it rotates on its axis and faster its satellites orbit. The only exception is the earth and its moon; we suspect this is due to the greater distance between the Moon and earth (384.4 x10 3 km) and Mars and its two moons (9.38 and 23.46 x10 3 km, despite the smaller sizes of the two moons of Mars.
*The masses for all the planets and earth’s moon were x10 24 kg and for the satellites of Mars were x 10 15 kg; for Jupiter’s moons were x 10 21 kg; for Saturn’s, Uranus’ and Neptune’s were x 10 20 kg. The above satellites are all synchronously rotating bodies (they rotate on their axes and orbit the mother bodies in the same time period and show only one face of the satellite to the mother).
Reproduced from J. High Energy Physics, Gravitation and Cosmology, 2021, 7, *-*, pp 1-25, https://www.scirp.org/journal/jhepgc (10)
The data presented in this table were adopted from https://nssdc.gsfc.nasa.gov/planetary/factsheet/

            Next let us examine axial rotations in the satellites. In Table 3 we present the data on masses of the same planets, and their axial rotation speeds as well as the distances of their synchronously rotating proximal satellites, the same ones as in Table 1 and the axial rotation speeds of the satellites. Once again, planets with multiple satellites show generally faster rotation of their satellites in rough correlation to the size of the mother body. Note the numbers in red, which are the averages for each planet’s satellites’ axial rotation speeds; here also there is a rough correlation between the speeds of rotation of satellites of larger planets vs those of smaller mother planets. Also, similar to the orbital speeds, the closer satellites tend to rotate faster than the farther out ones. So, here also, mother bodies’ size, its axial rotation speed and the satellite’s closeness to her have dominant effect on the synchronously rotating proximal satellites. This particular effect of mother bodies on satellites is uniquely educational in our understanding of the role of mother bodies’ axial rotation’s control of even the axial rotation of the close-by synchronously rotating satellites. In our next figures we will explore how mother bodies accomplish this feat.

TABLE 3
PLANETARY AXIAL ROTATION vs. SATELLITES’ AXIAL ROTATION SPEED
(Synchronously Rotating Satellites)

PLANETS

SATELLITES

MASS
(1024kg)

AXIAL ROT.
SPEED
(km/h)

MASS*

DIST. FROM
MOTHER
(103km)

AXIAL. ROT.
SPEED
(km/h)

MARS

0.642

867

PHOBOS
DEIMOS

10.6
2.4

9.38
23.46

9.33
1.25
=5.29

EARTH

5.97

1,677

MOON

0.073

384.4

16.7

URANUS

86.8

9,130

MIRANDA
ARIEL
UMBRIEL
TITANIA
OBERON

0.66
13.5
11.7
35.2
30.1

129.9
190.9
557
436
584

44
60.7
38
23.7
14.8
=36.24

NEPTUNE

102

10,231

NAIAD
THALASSIA
DESPINA
GALATIA
LARISSA

0.002
0.004
0.02
0.04
0.05

23.2
25.2
27.7
37.2
48.8

31.5
36.9
60.5
54.3
47
=46.04

SATURN

568

17,775

MIMAS
ENCELADUS
TETHYS
DIONE
RHEA

0.379
1.08
6.18
11.0
23.1

185.5
238
294.7
377.4
527

51.6
44.5
40.8
36
30.7
=40.72

JUPITER

1899

42,255

IO
EUROPA
GANYMEDE
CALLISTO

893.2
480
1481.9
1075.9

421.6
670.9
1070
1883

269.6
115.2
95.7
37.8
=129.58

Data in this table were adapted from http://nssdc.gsfc.nasa.gov/planetary/factsheet and related pages. Only for the moon was actual values derived from NASA’s website; all other values were calculated from the values for the orbital parameters posted on that site. For calculating the axial rotation speeds, either using the ‘median axisradius’ given by NASA, or by calculating it from the data provided (for the small satellites, where their shapes are not spherical) were used to determine the circumference. Since the satellites were synchronously rotating, for axial rotation period, the orbital period was used. Then, the satellites’ orbital rotation was calculated from the two values. * The masses for satellites of Mars were x10 15 kg; for moon it was x10 24 kg, for Uranus’, Neptune’s and Saturn’s were x10 20 kg; for Jupiter’s they were 10 21 kg.
Reproduced from J. High Energy Physics, Gravitation and Cosmology, 2021, pp 1-25, 7,*-*, https://www.scirp.org/journal/jhepgc (10)

In Figure 2 below, we explain how mother bodies may be influencing the axial rotation of the proximal satellites. Shown in the figure are schematic representation of three synchronously rotating large moons (“Galilean moons”) of Jupiter. These are totally fictional and not rendered in proportion and the figure is meant to convey the idea of how axial rotation of this mother body is aiding the axial rotation of the satellites. The collaboration between mutual gravitation and axial rotation can be described as a combination of the dominant gravitation from the mother interacting with the satellite’s body in such a way that when the mother rotates on her axis, the satellite moves in the same direction. And as the satellite is thus orbiting, its advancing front end experiences tug from the mother’s gravitational pull. This is what augments the satellite’s own axial rotation. The closest satellite (numbered 1) is already orbiting and rotating on its axis faster than the other two satellites that are positioned farther away from the mother, Jupiter. The second and third satellites experience the same tug at their own advancing front end, albeit in slightly reduced strength, which depends on the distance from the mother. We wish to stress that the whole body of the satellites also experience pull from the mother and those tugs help keep the mother’s hold on the satellite(s); only the tug ahead of the advancing front end gets a rotational pull from the mother. While we showed in this figure only Jupiter and three synchronously rotating satellites, all such satellites of gas giants (Jupiter and Saturn) and ice giants (Uranus and Neptune), all of whom have multiple satellites, also display the same pattern and the same explanation can be applied to all of them.

Figure 2. A gas giant and three of its synchronously rotating major satellites.
Reproduced from Applied Phys. Res. Vol. 12, No.2, 2020 http://dx.dol.org/10.5539/apr.c12n2p1(11)

Figure 3. The mechanisms underlying the “Negative” rotation of the planet Venus and the inordinate delay in its axial rotation. This unusual phenomenon also aids in our understanding of how axial rotation and gravity work in tandem to create celestial body motions. In the case of Venus, Pluto and all the peripheral small satellites of gas and ice giants of the solar system, the result of their interactions is, in contrast to the synchronously rotating proximal satellites, that of slowing of the bodies’ axial rotation. One crucial finding that has bearing on that resultant odd motion characteristic is that all these bodies’ axes are tilted considerably more than 120 degrees. In fact, Venus is tilted -174 degrees. Therefore, all these bodies superficially appear to rotate in the clockwise direction; however, that is an illusion created by excessively tilted axis. They are, in fact, rotating on their axes in the counterclockwise direction and all of them rotate very slowly. Venus, which is almost upside down (the South Pole is at the top and North Pole is at the bottom) is the extreme example of this phenomenon. The question is, why do they rotate very slowly but continue to orbit at the appropriate speed as dictated by Newton’s inverse square law? To understand the principles of this unique motion characteristic, please refer to our explanation of the synchronous rotation above in figure 2. In reference to figure 3, the tug experienced at the advancing front end of Venus from Sun is to coax the planet to rotate in the counterclockwise direction. However, Venus’ impulse is to spin exactly in the opposite direction. Thus, there is conflict between the Sun and Venus, and this explains the inordinate delay in Venus’ axial rotation (-5832.6 hours). All other inverted bodies experience similar influence from mother bodies but based on their respective axial tilt, the delay would be somewhat less in degree.

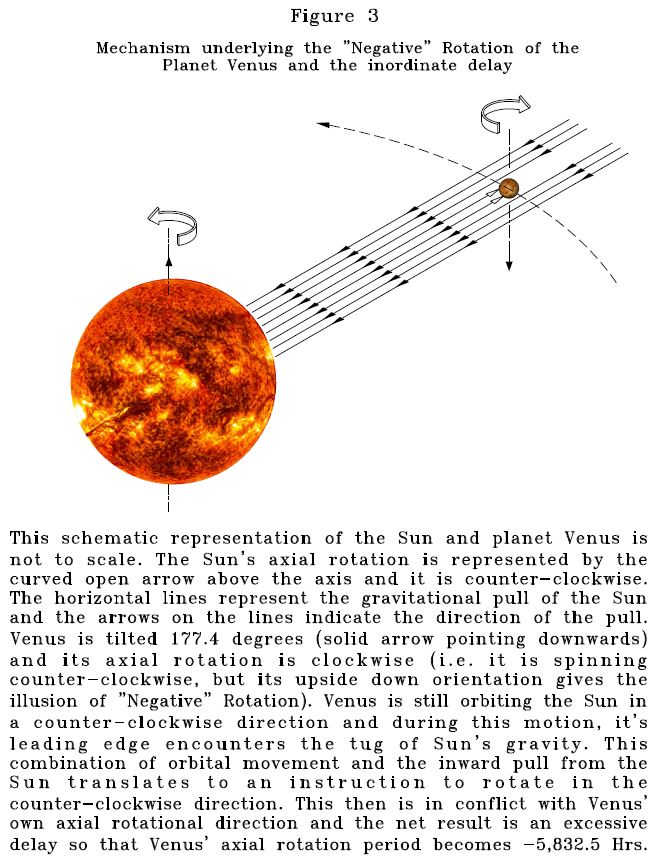
Reproduced from Appl. Phys. Res. Vol. 12, No. 2, 2020; http://dx.doi.org/10.5539/apr.v12n2p1 (11)

Table 4 below lists the satellites of Jupiter to examine the motion characteristics of its satellites. The satellites of the other gas giant Saturn and those of the two ice giants Uranus and Neptune display almost identical pattern of motion characteristics. Thus, this table is uniquely instructional in learning the roles played by distance from mother bodies in our solar system, in terms of speed of orbit and, of special interest to us, the speed of axial rotation of the satellites. The closest large moons, from Io to Thebe display the least axial tilt (less than 2 degrees) are in synchronous rotation; those satellites that are in intermediate distances from Jupiter, Themisto to Valetudo (between 27.35 to 51.4 degrees) display nonsynchronous or normal rotation, and the farthest, tiny satellites, from Euporie to S/2003 J23 (axial tilts between 139.8 to 166.7 degrees) are rotating inversely and extremely slowly(550.7 to 779.2). While it is easy to explain why the axis tilts with distance from Jupiter, why after a certain distance they uniformly become almost inverted, is hard to explain. We explained this in our prior paper 8. Briefly, we think that the axial tilt is influenced also by the diminishing electromagnetic discharge from Jupiter and the inversion hints at a reversal of polarity. However, this needs to be scientifically studied and proven or disproved.

_________________________________________________________________________________________

TABLE 4

ORBITAL PARAMETERS OF SATELLITES OF JUPITER

Satellite. Radius. Dist. from Orbital Period. Rot. Period. Inclination

(Degrees) (km). Jupiter. (Days). (10 3 km)

________________________________________________________________________________

Galilean

Io 10821 421.8 1.769138 S 0.04

Europa. 1560.8 671.1 3.551181 S 0.09

Ganymede. 2531.3 1070.4 7.154553 S 0.18

Calisto 2410.3 1882.7 16.689017 S 0.19

Lesser Satellites

Metis 30 x 20 x 17 128.0 0.294779 S 0.02

Andrastea 10 x 8 x 7 129.0. 0.298260 S 0.05

Amalthea 125 x 73 x 64. 181.4 0.498179 S 0.38

Thebe 58 x 49 x 42 221.9 0.6745 S 1.08

__________________________________________________________________________________________

Themisto. 45 7507 130.02 N 43.08

Leda 9 11165 240.92 N 27.46

Himalia 85 11461. 250.5662 N 27.50

Ersa. 1.5 11483. 252.0 N 30.61

S/2018 12. 1.5. 11490. 252.0 N 29.4

Pandia 1.5 11525. 252.1 N 28.15

Lysithea (X). 12 11717. 259.22 N 28.30

Elara (VII). 40 11741. 259.65 N 26.63

S/2011 J3 1.5 11829 263.0 N 28.7

Dia 2.0 12118 287.0 N 28.2

S/2018 J4. 1.0 16549. 434.7 N 53.2

Carpo 1.5 16989 456.1 N 51.4

Valetudo 0.5 18980 533.3 N 34.0

__________________________________________________________________________________________

Euporie 1.0 19302 550.7 R 145.8

S/2003 J18 2.0. 20274. 588.0 R 146.4

S/2010 2.0 20307 588.1 R 150.4

S/2003 J16 2.0. 20567 598.6 R 151.1

S/2003 J2 2.0 20610 602.3 R 149.2

S/2017. 1.0. 20627. 602.6 R. 143.4

S/2016. 0.5 20651. 602.7 R. 139.8

S/2017 1.0 20694 606. R 147.9

Orthosis 1.0 20721 622.6 R 145.9

S/2021 J1 0.5 20723 606.4 R 149.8

Euanthe 1.5 20799 620.6 R 148.9

Thyone 2.0 20940 627.3 R 148.5

S/2022 J3 1.0 20968 617.3 R 144.5

Mneme 2.0 21069 620.0 R 148.6

Harpalyke 2.2 21105 623.3 R 148.6

Hermippe 2.0 21131 633.9 R 150.7

Praxidike 3.4 21147 625.3 R 149.0

Thelxinoe 2.0 21162 628.1 R 151.4

S/2021 J2 0.5 21198 627.8 R 150.1

Eupheme 2.0 21200 627.8 R 148.0

Helike 4.0 21263 634.8 R 154.8

Iocaste. 2.6 21269 631.5 R 149.4

Ananke (XII). 14.0. 21276 610.5 R 148.9

S/2017 J9 1.5. 21487 639.2 R 152.7

S/2021 J3 1.0. 21615 642.8 R 150.1

S2003 J12 1.0 21615 646.0 R 154.7

S/2022 J1 1.0 22074 668.4 R 165.4

S/2003 J4 2.0 22110 668.0 R 149.4

S/2016 J3. 1.0 22273 675.7 R. 164.1

S/2017 J6 1.0 22455 683.0 R 155.2

S/2011 J1. 1.0 22462 686.6 R 163.3

S/2022 J2 1.0 22473 686.7 R 165.4

S/2003.J19 2.0 22757 697.6 R 166.7

Philophrosyne. 2.0 22820 701.3 R 143.6

Eurydome. 1.5 22865 717.3 R 150.3

S/2018. J3 0.5 22888 704.9 R 164.9

S/2021 J5 1.0 22893 704.9 R 163.2

S2003 J10 2.0 22918 704.9 R 163.0

Arche 1.5 22931 723.9 R 165.0

S/2021 J4 0.5 22950 708.6 R 164.0

Autonoe 2.0. 23039. 762.7 R 152.9

Pasithee. 1.0 23096 719.5 R 165.1

Herse 2.0 23097 715.4 R 164.2

S/2003 J24 1.0 23150 715.9 R 162.1

Chaldene 1.9 23179 723.8 R 165.2

Kale 1.0 23217 729.5 R 165.0

Isonoe. 1.9 23217 725.5 R 165.2

Altne 1.5 23231 730.2 R 165.1

S/2017 J5 1.0 23232 719.5 R 164.3

S/2017 J8 0.5 23233 719.6 R 164.7

Erinome 1.6 23279 728.3 R 164.9

S/2017 J2. 1.0 23303 723.1 R 166.4

S/2010 J1 1.0. 23314 723.2 R 163.2

Taygete 2.5 23360 732.2 R 165.2

Carme 23 23404 702.3 R 164.9

S/2011 J2 0.5 23464 730.5 R 148.8

Sponde 1.0 23487 748.3 R 151.0

S/2021 J6 0.5 23490 734.1 R 166.5

S/2017. J1 1.0 23547 734.2 R 149.2

Kalyke 2.6 23583 743.0 R 165.2

Pasiphae. 29 23624 743.6 R 151.4

Euketade. 2.0 23661 746.4 R 165.5

S/2016. J4 0.5 23728 743.7 R 146.3

Elrene. 2.0 23732 759.7 R 163.2

Megaclite 2.7 23806 752.8 R 152.8

Sinope 19 23947 739.6 R 155.2

Aoede 4.0 23981 761.5 R 158.3

Kallichore 2.0 24043 764.7. R 165.5

Callirrhoe 3.5 24102 758.8 R 147.1

S/2003 J9 1.0 24234 766.5 R 166.3

Cyllene 2.0 24349 737.8 R 149.3

Kore 2.0 24543 779.2 R 152.4

S/2003 J23 2.0 24750 759.7 R 146.1

This table is adapted from http://nssdc.gsfc.nasa.gov/planetary/factsheet/joviansatfact.html

Last updated 18th March 2025

The data printed in the top section apply to the most proximal satellites, with the least axial tilt (less than 2 degrees) and are rotating synchronously; those in the middle section with axial tilts between 26.63 and 51.4 degrees are rotating non-synchronously, and the most numerous, the most peripheral and the smallest satellites are in lowest group, their axes are tilted the most ( between 139.8 and 166.5 degrees) and are rotating negatively.

S= Synchronous rotation, the rotation period is the same as the orbital period

N= Nonsynchronous or normal rotation

R= Retrograde or Negative rotation

Table 5: The data for this table were derived from published material online, mainly from Wikipedia.org but, some were confirmed or corrected by values posted on other sites, as well as from nasa.gov website. The table compares the equatorial radii, masses, distances from earth, radial velocities (the stars’ movement across the galaxy), and the speeds of the axial rotation of a selection of stars in the Milky Way Galaxy; the stars were randomly selected based mainly on their radii compared to those of our sun and listed in increasing order of distances from earth. The only other consideration was the availability of essential data such as mass, radius, radial velocity and rotational velocity. Although there is a definite suggestion of increased axial rotation rates with the masses and radii, when both the radii and masses are similar, (stars 1-15, 19 and 23) it is not strictly linear. It is also noteworthy that both the availability of complete data and similar values of masses and radii are in stars that are the closest to the sun. This means the readings are more accurate and more available for close-by stars. When the radii and masses do not correspond, which also are in stars that are much farther away, the rotational values are quite unpredictable. Even so, one does notice larger rotational speeds in larger stars (stars 18, 19,20, 33). We infer from the above that the farther away the stars are from the observers, the less accurate the readings are. Therefore, only with more accurate readings in the future can we have conclusive evidence for the patterns of stars’ behavior. In general, we believe, the data presented in this table does not refute our contention that the larger a star, faster it will rotate on its axis.

TABLE 5
SELECTED PARAMETERS OF STARS IN SUN’S NEIGHBORHOOD

STAR	DISTANCE (Light Years)	RADIUS*	MASS*	RAD. VEL Km/Sec	ROT. VEL Km/Sec
1)Prox.Centauri	4,24	0.154	0.122	-22.20	<0.1
2)Alph.Centauri	4.37	1.22	1.1	-21.4	2.7+-0.7
3)Alph.Centauri	4.37	0.86	0.907	-18.6	1.1+-0.8
4)Barnard’s star	5.96	0.196	0.144	-110.6	<2.5
5)Wolf 359	7.86	0.16	0.09	+19	<3.0
6)Sirius A	8.6	1.71	2.063	-5.5	16
7)Luyten 726-8	8.73	0.14	0.102	+29	28.2
8)Ross 154	9.6	0.24	0.17	-10.7	3.5
9)Ross 248	10.29	0.16	0.136	-75.2	1.2
10)Ross 128	11	0.197	0.168	-31	N/A
11)61 Cygni A	11.4	0.665	0.7	-65.9	N/A
12)61 Cygni B	11.4	0.595	0.63	-64.4	N/A
13)Procyon A	11.46	2.05	1.50	-3.2	3.16
14)Epsilon Indi	11.87	0.732	0.754	-40.4	1.46
15)Vega	25	2.36x2.8	2.1	-13.9	20.48
16)Arcturus	36.7	25.4	1.08	-5.19	2.4
17)Aldebaran	65.3	44.13	1.16	54.26	3.5+-1.5
18)Beta Carinae	113.2	6.8	3.5	-5.2	145.7
19)Achernar	139	7.3x11.4	6.7	+16	250
20)Alpha Arae	270+-20	4.5	9.6	0	375
21)Canopus	310	71	8	+20.3	9
22)Polaris	323-433	37.5	5.4	-17	14
23)Pleone	392	3.2	3.4	+4.4	329
24)Epsilon Aurig	653-1500	143-358	2.2-15	10.4	54
25)PZ Cassiopei	2810	1062	N/A	-45.68	45
26)Rho Cassiopei	~3400	636-981	40	-47	25
27)VY Canis Major	~3820was p	1420	17	41	300
28)KY Cygni	~3600	672	25	N/A	N/A
29)UY Scuti	~5100	755	7-10	+18.33	18
30)V382 Carinae	5930	485	20	+6	57+-15
31)V915 Scorpii	5436	760	N/A	+46	N/A
32)Eta Carinae	7500	~240	120-200	-25	N/A

This table is reproduced from Applied Science and Innovative Research, Vol. 4, No.3, http://dx.doi.org/10.22158asir.v413p1

In Table 6 below we present galaxies of different sizes and distances from observers on earth; the data were derived from our review of astronomy/astrophysical journals and various online sites, including nasa.gov, Wikipedia.org and others. There is great paucity of data for the parameters we were particularly interested in (axial rotation speeds and radial velocity vs mass/size of the galaxies). We tried to select large galaxies and compare them with medium-sized ones such as our Milky Way Galaxy. Apparently, the largest of the galaxies are also the farthest and clearly the availability of data is severely hampered by that fact alone. Thus, on this table we were left with comparison of only a few galaxies (nos. 1,6,7,8 vs 10&11). Even with this sparse data, there is a good hint that the galacto-radial and helio-radial velocities are higher; the larger the galaxy is. Taken together with the recent observations of the "Super Spirals" (12) rotating faster, we can safely predict that future availability of accurate information will confirm our belief. We have discussed two observations pertaining to the motion characteristics of spiral galaxies that were baffling to the scientists and how our discoveries on how the mutual gravitation and the axial rotation of bodies interact can explain them adequately; examples are why the stars near the center of the galaxies were seemingly moving at around the same speed as those in the periphery and why the arms of the spiral galaxies do not fly away as a consequence of the extreme rapidity of the axial rotation of the galaxies. (Please refer to the appropriate section for details).

TABLE 6

SELECTED PARAMETERS OF LARGE GALAXIES
Name	Distance (LY)	Mass*	Size (Diam.) (LY)	No. of Stars	Helio-Radial Vel (Km/s)	Galacto-Centric Vel (Km/s)
1) 1C 1101	1.045 ± 0.073 B	N/A	4M	100 T (1014 )	23,368 ± 26	23,395 ± 26
2) 3C 348 (Hercules A)	2.1 B	1,000 *	1.5M	N/A	N/A	N/A
3) A2261 – BCG	3 B	10 *	1M	10 T (1013)	N/A	N/A
4) ESO 306 – 17	493 M	2.5 arc. Sec	1M	N/A	N/A	N/A
5) UGC 2885	232 M	463 K ly	800	1T	N/A	N/A
6) Comet	3.2 B	3.8 x 108 M⊙	600K	N/A	3.4M	N/A
7) NGC 6872 (Condor Gal)	212 M	>1011 M⊙	522K	N/A	4,555	4,443
8) ESO 444 – 46	640 M	10,000 *	402K	N/A	14,061	N/A
9) Tadpole	420 M	N/A	280K	N/A	N/A	N/A
10)Andromeda	2.54 M	1.76 *	~220K	1T	-301	- 120
11) Milky Way	_______	1x1012 M⊙	105.2	250-500	210	N/A

LY= Light years K= x1000 M= Million B= Billion T= Trillion
N/A = Data not available
⋆ = x Mass of Milky Way Galaxy
M⊙= x Mass of Sun
This Table and the accompanying legend are reproduced from Journal of High Energy Physics, Gravitation and Cosmology (2023). 7, *.* https://www.scirp.org/journal/jhepgc

DISCUSSION
The core facts presented in this paper were garnered from readily available data from the astronomy and astrophysics literature and from the websites of NASA and other organizations. They were, in fact, hiding in plain sight, but our search unearthed them simply because of the pointed search we conducted. The result of our search can be surmised as follows: In the macro world, simply by the fact that a body is more massive, the faster it is able to rotate on its axis. This increased speed of rotation of larger mother bodies affords them the ability to make the close by synchronously rotating satellites both orbit and rotate on their axes faster. One can also see a direct effect of distance from mother bodies, in the axial rotation speed of satellites. The mechanism involved in the negative or reverse rotation of planets and satellites whose axes are tilted excessively gives us a unique view into how the mother bodies’ rotation influences the satellites’ rotation. In the classic example of Venus, its appropriate counterclockwise axial rotation runs afoul of instructions from the Sun to do exactly the opposite (because of Venus’ inverted axis) and thus results in inordinate delay of the axial rotation of Venus. However, the orbital speed is not affected; thus, this is a crucial hint that the rotational instructions from mother bodies have a direct effect in the rotation dynamics.

The effect of distance from mother bodies and the motion characteristics of their satellites in the solar system can be illustrated by the data presented in Table 4. The system shown in the table is of Jupiter and its satellites. However, the other gas giant Saturn and the two ice giants Uranus and Neptune and their respective satellites display a very similar pattern. The closest large moons have very low axial tilts and rotate synchronously; these are satellites Io to Amalthea (axial tilts 0.04 to 0.10); those satellites that are intermediate in distance, display nonsynchronous or normal rotation. These satellites are Themisto to Carpo (their axial tilts are between 45.67 and 51.4 degrees). Finally, those satellites that are farthest from Jupiter, Euporie to Autonoe (axial tilts 145.9 to 165.5) and they display negative rotation and considerable delay in their axial rotation. This pattern suggests diminishing axial rotational influences from Jupiter to its satellites, depending on the distance. We believe that at least in part the axial tilt progressing with distance also reflects diminishing magnetic force of the mother and, once the tilt goes over 140 degree or so, negative rotation results, and definite slowing of their speed of rotation; see the spread from 553.1 in Kore to 779.2. The negative rotation and delay in axial rotation in these farthest small satellites is reminiscent of what is noted in axially inverted planets like Venus.

When one considers the presence of axial rotation in fundamental particles, as well as in the largest congregations of matter, the galaxies, the protoplanetary disk and all freestanding celestial bodies, it is not difficult to conclude that it must have some purpose. This feeling was one of the motivating factors of our search of the literature. We soon came to the conclusion that the notion that “conservation of the angular momentum” is simply an observation and not necessarily of any consequence or purpose was wrong, and needlessly it impeded the progress of this field of science. Next, our focus turned to the role of the equally ubiquitous presence of mutual gravitation; originally described by the great Indian astronomer/mathematician Varahamihira ( ) and reaffirmed by Isaac Newton ( ). However, we were skeptical about the notion that mutual gravitation alone or even the addition of Newton’s 1st law of motion9 could explain the motion mechanics adequately. For example, they couldn’t explain the orbits of satellites being only in the counterclockwise direction, and only along the ecliptic of the mother bodies, not to mention all the fluid axial rotations of mother bodies interacting with and directing the axial rotations of the satellites. We also recognized that Einstein’s “warping of the space” 10 around large bodies also could not explain any of the orbital or axial rotational movements. Our discoveries explain how the fundamental forces in nature are structured to work together and efficiently, without leading to constant chaos in the universe. Below, we will examine different areas of astronomy where the motion mechanics and some related phenomena are explicable efficiently by applying the principles we have outlined throughout this article.

By connecting the nanoworld of atoms and fundamental particles with the macroworld of planets, their satellites and stars and galaxies, the demonstration that the motion mechanics are the same everywhere, we can recognize this property as a universal behavior of matter.
It explains why even at the outset of star formation and its satellite bodies that are embedded in the protoplanetary disk, the same counterclockwise axial rotation is manifested by the disk. Note should be made of the fact that not only the star and the protoplanetary disk are rotating in the counterclockwise direction, but also all the myriad bodies contained in the system do so.
The origin of motions of all bodies can be traced to the intrinsic axial rotation of matter; the larger the body the faster its rotation. Thus, in the solar system, the satellites rotate at rates of 9.33-269.6 km/hour, while their mother bodies, the planets rotate from 867 to 45,455 km/hour. The infinitely larger, stars and galaxies, on the other hand, rotate on their axes in 0.1-210 km/second and 210-23,368 km/second respectively!
It explains how gravity manifests its effects on celestial bodies of sufficient size by imparting spherical shape, and by melting the matter deep inside the body helps make electromagnetism 6.
It teaches us how synchronous and negative rotations occur 8. Please refer to the text for details.
The odd behavior of Triton: Triton is a close-by large moon of Neptune that is orbiting the mother in the clockwise direction, while Neptune is rotating on its axis and orbiting the sun in the counterclockwise direction. Since the orbits of satellites should always follow the axial rotation of mother bodies, as that is the mechanism behind orbits, we suspect there is an unknown gravitationally active body, such as an undiscovered planet that is in the vicinity that keeps Triton held in one place, due to its and Neptune’s and Uranus’ gravitational tugs such that, the arrangement gives the illusion of Triton orbiting in the wrong direction, against the normally (counterclockwise) rotating Neptune (11).
It explains the extreme speed of orbit of some exoplanets that are orbiting close to their star(s); these may be examples of synchronously rotating planets (13). Again, our knowledge that the closest satellite bodies) will show synchronous rotation helps explain this phenomenon, which is not seen in our solar system (17)
It explains how the stars and the greatest congregations of matter, the galaxies, are able to rotate on their axes so fast, and why the larger galaxies rotate even faster. The latter go by the nickname, “Super Spirals”12 Again, the natural ability of collections of matter to rotate on its axis, and for larger congregations to rotate faster explains these findings adequately.
Why stars near the center of galaxies move at around the same speed as the ones in the periphery. We think careful analysis will find that the farthest stars are moving faster than the nearer ones, as they have to catch up with the closer stars, as they complete each turn of the galaxy 7. We have explained in our paper that the odd behavior is because when it comes to galaxies, Newton’s inverse square law does not apply to such tremendous collections (hundreds of billions of stars) of extremely gravitationally active bodie; the whole galaxy behaves like a rotating tabletop and thus all stars move roughly at the same speed.
Why spiral galaxies’ arms flare out, and yet why they do not fly away during the high-speed rotation of the galaxies. The arms of the galaxies, which are brimming with billions of gravitationally active stars, and each arm is situated parallel and close to neighboring arms (in astronomical terms), the gravitational pull between these arms will exert an inward pull on the neighbors such that it neutralizes the centrifugal force of rotation.
Why do some galaxies collide with other galaxies? In the current belief in cosmology that all galaxies are hurtling through the universe outwardly away from one another, it is impossible to explain how any galaxy can bump into other galaxies. Our proposal is that the galaxies move in space in the counterclockwise direction and larger galaxies rotate on their axes and move in space faster than the smaller ones, the larger ones will likely overtake the smaller ones and that is the way these collisions take place. We have a good example with our galactic neighbor Andromeda, a far bigger galaxy pursuing our Milky Way Galaxy. We can see how these collisions thus only take place from behind. This has been explained at length in one of our prior paper7..
Explain why the light from far away galaxies are more redshifted can be explained satisfactorily by applying our discoveries described in this paper. The traditional explanation that this redshift phenomenon is due to expansion of the universe, where all bodies are hurtling outward and away from one another in a straight line is inconsistent with both how bodes move (in a circumferential manner) and also in the not infrequent collisions between or merging of galaxies. One would not expect such collisions when all bodies are flying away from one another. In contrast, our findings can explain both findings elegantly. First, since the larger galaxies are moving faster than the smaller ones, the former can frequently overtake smaller galaxies from behind. We explain the increased redshift this way: since the galaxies are rotating on their axes in the counterclockwise direction, to an observer’s instruments the receding arms could present the picture of the whole galaxy moving away, and for objects that are so incredibly far away, our feeble instruments are fooled. If the galaxies were rotating in the clockwise direction, on the other hand, the flaring ends of the arms might give the illusion of the whole galaxy as being moving towards the observer, and thus blue-shifted.
It explains how the stars and the greatest congregations of matter, the galaxies, are able to rotate on their axes so fast, and why the larger galaxies rotate even faster, again, without resorting to unseen, undetectable, mathematical constructs such as black holes, supermassive or not, Dark matter15,16 “WIMPs”17 “MACHOs”16,”Axions”18, Black haloes19 and so on. Even the rotational motion capability of spiral and elliptical galaxies can be explained by the ability of the central very luminous body's innate ability to rotate on its axis and carry the rest of its load of stars with it. These bodies, which are either in a spherical or bar-like shape, we think are billions of stars that have coalesced and become one huge star-like but much larger unit, that is thus empowered with the ability to rotate at enormous speeds, as we have touched upon in the text. We would like to stress that the job of rotating the whole galaxy on its axis by this central body is made much easier by the weightlessness of the whole galaxy and by the vacuum that prevail in the deep space, and the weightlessness of even the whole galaxy.
Why the circumferential and counterclockwise motion of the galaxies will give the illusion that the universe is spinning on an axis. In a prior paper we have explained how this illusion appears7. We have suggested that the counterclockwise rotation of the spiral galaxies will set in motion a movement across space also in a circumferential manner and in the counterclockwise direction. We believe the rotational movement of the galaxies will propel them through space in the manner that resembles the motion of frisbees once they are launched.

CONCLUSION

Many of the discoveries that we have unearthed from current scientific literature are self-evident and do not need experimental validation. Such are the control mother bodies have in both directing and controlling their satellites’ orbital direction and speed, as well as the speed of axial rotations of their most proximal synchronously rotating larger satellites. Also obvious is the transition to nonsynchronous and then reverse rotations of these bodies, simply because of the distance from the mother. Some others would need observations done in close proximity to the bodies, far away from earth. One such is to check the magnetic polarity shift of mother bodies, in locations where the tiny, most distant negatively rotating and inversely tilted satellites are situated. Another is checking the polarity of Kuiper Belt Objects; if our hypothesis is correct, most, if not all such peripheral small “dwarf planets/planetismals” will display inversion of their axes to varying degrees beyond 120 degrees or so and slow axial rotation.is that the farthest satellites of stellar systems will mimic that of the large planets and their satellite systems is correct, all or vast majority of them will display this. Next a search at locations between Neptune and Uranus for a gravitationally active large body, perhaps an unknown planet. Yet another, but much more difficult observation is on the large exoplanets (some are the size of Saturn and Jupiter) that have been found to orbit their star very close to and orbiting extremely fast and completing each orbit within 3 or 4 earth days. We have speculated in this paper that such planets are likely synchronously rotating planets. Yet another observational proof is to study the direction of lateral motions of galaxies; most of them will be counterclockwise in the Northern Hemisphere and clockwise in the Southern Hemisphere; this is because the southern galaxies are upside down, from our vantage point. A related observation will be how collisions between galaxies occur; by our estimation, all collisions will be by larger galaxies colliding or merging with smaller galaxies from behind, and not head on or from the side. Finally an experiment that will offer evidence for the spontaneous onset and persistence of axial rotation in free-standing celestial bodies. These should be conducted in deep space, where conditions are right for such motions; almost friction-free vacuum, weightlessness as there are no gravitationally active bodies nearby, and the extreme cold in those locations. If balls of different sizes and made of different materials, with one hemisphere painted while and the other one black and containing a bar magnet of the appropriate length for the ball (to mimic what happens to planets and satellites) are released, we predict the balls will spontaneously begin to rotate on their “axis” and continue to do so indefinitely.

REFERENCES

Gasioorowicz, S, and Langacker, P (2005). Elementary Particles in Physics. Dept. of Physics and Astronomy, Univ. of Pennsylvania. https://www.physics.upenn.edu>~pgl
Franke-Arnold, S: Optical Angular Momentum and Atoms. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. (2017). https://doi.org/10.1098/rsta.2015.0435
Padgett, M, and Allen, L. Light with a Twist in its Tail. Contemporary Physics (2010). Vol. 41, number 5, pages 275-285. https://doi/org/10.1080/00107510075001277
Pearce, I.G. Indian Mathematics-Redressing the Balance. The Classical Period: II Aryabhata and His Commentators. https://mathshistory.st-andrews.ac.uk/Projects/Pearce/chapter-10
Kour, B, and Singh, B. Ancient India’s Mathematical Marvel: Aryabhata’s Enduring Global Influence-Analysis. https://www.eurasiareview.com/19122024-ancient-indias-mathematical-marvel-enduring-global-influence-oped/
Aryabhata: www.britannica.com/biography/Aryabhata-1
Hayashi, T. Aryabhata’s Rule and Table for Sine-Differences. Historia Mathematica 24(1997), 396-406, Article No. HM972160. https://core.ac.uk/download/pdf/8251881.pdf
Kak, S. Aryabhata’s Mathematics. RSA Conference, San Jose, Feb. 13-17, 2006. www.researchgate.net/publication/45901748_Mathematics
Raghuprasad, P.K. (2020) Spin: Ubiquitous, Fundamental, Purposeful: Its Complementary Interactions with Gravity. Applied Science and Innovative Research. Vol.4, No.3. http://dx.doi.org/10.22158/asir.v413p1
Raghuprasad, P.K. (2021) Pivotal Role of Spin in Celestial Body Motion Mechanics: Prelude to a Spinning Universe. J. High Energy Physics, Gravitation and Cosmology, https://www.scirp.org/journal/jhepgc
Raghuprasad, P.K. (2020) Synchronous, Nonsynchronous and Negative Rotations: How Spin and Gravity Orchestrate Planetary Motions: Applied Physics Research, Vol. 12, No.2, 2020. Doi :10.5539/apr.v12n2p1 URL:http://dx.doi.org/10.5539/apr.v12n2p1

12)Pearce, I.G. https://mathshistory.st-andrews.ac.uk/Biographics/varahamihira/
13)Seeds, M.A, Stars and Galaxies (Wadsworth, Belmont, CA, 1999), p. 82
14)Einstein, A. (1920). The Special and General Theory (Random House, New York,)
15)Raghuprasad, P.K. Planetary Spin-Orbit Attributes in the Solar System and their Wider Implications. Physics Essays, 26,2,2013
16)Ogle. P.M, Jarrett. T, Lanz. L, Cluver. M, Alatalo. K, Appleton. P.N, Mazzarella. A Break in Spiral Galaxy Scaling Relations at the Upper Limit of Galaxy Mass. (2019)The Astrophysical Journal Letters, 884, L11. https://doi.org/10.3847/2041-8213/ab459e
17)Wang. J, Fischer. D.A, Horsch, E.P, and Huang, X. (2015) On The Occurrence Rate of Hot Jupiters in Different Stellar Environments. The Astrophysical Journal, 799(2). https://doi.org/10.1088/0004-637X/7922929
18)http://nssds.gsfc.nasa.gov/planetary/factsheet.neptune
19)deSwart, J.G, Bertone.G, van Dongen.J. (2017) How Dark Matter Came to Matter. Nature Astronomy. 1(59). 0059 https://doi.10.1038/s41550-017-0059
20)Tisserand. P, Le Guillou, Alfonso, H.N et al (2007). Limits on the Macho Content of the Galactic Halo from the EROS-2 Survey of the Magellanic Clouds. https://doi.org/10.48550/arXiv.Astro-ph/0607207
21)Jungman, G, Kamionkowski. M, Griest. K. (1996). Supersymmetric dark matter. Physics Reports. 267(5-6). 195-373 https://doi.org/10.48550/arXiv.hep-ph/9506380
22)Peccei. R.D, (2008). The Strong CP Problem and Axions. In Kustner, M. Raffles, G. and Beltran Berta (eds). Axiions: Theory, Cosmology and Experimental Searches. Lecture Notes in Physics. Vol. 741, pp https:/doi.org/10.48550/arXiv.hep-ph/0607268
23)Jog, C.J (2002) Large Scale Asymmetry of Rotation Curves in Lopsided Spiral Galaxies. Astronomy and Astrophysics, 391, 471-479. https://doi.org/10.1051/0004-6361:20020832